I still remember the first time the Unit Circle felt less like a diagram and more like a quiet companion, sitting there on the page, patient, round, almost breathing.
It was early, my coffee had gone cold, and the notebook smelled faintly of pencil wood. Math doesn’t always arrive with trumpets. Sometimes it tiptoes in, wearing socks, asking if you’re awake enough to listen.
This is one of those topics. The Tangent doesn’t shout either, it sort of leans, tilts, explains itself sideways. If you’ve ever felt intimidated by Trigonometry, or thought the circle was judging you, don’t worry, it kinda judges everyone at first, then it softens.
This article isn’t here to rush you. We’re going to walk slow, maybe take a wrong turn or two, because that’s honestly how understanding sticks. And yes, there will be Examples, but not the stiff kind that feel like they’re wearing suits. More like examples that sit next to you and say, hey, let’s figure this out together, yeah?
| Concept | Short Definition | Key Formula / Meaning | Quick Example |
|---|---|---|---|
| Unit Circle | A circle centered at origin with radius = 1 | Radius = 1 unit | Center at (0,0) |
| Radius of Unit Circle | Distance from center to any point | Always equals 1 | From (0,0) to (1,0) |
| Angle (θ) | Rotation from positive x-axis | Measured in degrees or radians | 30°, 45°, π/2 |
| Cosine (cos θ) | x-coordinate on unit circle | cos θ = x | cos 60° = 1/2 |
| Sine (sin θ) | y-coordinate on unit circle | sin θ = y | sin 30° = 1/2 |
| Tangent (tan θ) | Ratio of sine to cosine | tan θ = sin θ / cos θ | tan 45° = 1 |
| Tangent on Unit Circle | Represents slope of angle | Undefined when cos θ = 0 | tan 90° = undefined |
| Trigonometric Functions | Functions from angles to numbers | sin, cos, tan | Used in trig problems |
| Coordinate Point | Location on unit circle | (cos θ, sin θ) | At 45° → (√2/2, √2/2) |
| Use in Trigonometry | Defines trig values for all angles | Works for all θ | Solving angles & ratios |
The Definition of Unit Circle, Told Without Stiff Shoes
At its core, the Definition of Unit Circle is almost suspiciously simple. A circle. Centered at the origin. With a Radius of exactly one unit. That’s it. That’s the whole dramatic reveal. In the coordinate plane, this means every point on the circle is exactly one unit away from (0,0). The unit radius is the star of the show here, quietly making everything else possible.
But here’s where it gets interesting, and a little messy, in a good way. This circle becomes the stage on which all the Trigonometric Functions perform. Sine, Cosine, and yes, our slightly rebellious friend, Tangent, all get defined using this circle. The angle, usually called θ because mathematicians like Greek letters for reasons we won’t question today, starts at the positive x-axis and spins counterclockwise. Every position of that angle touches the circle somewhere, and that touchpoint becomes data. Real, usable, sometimes confusing data.
A retired teacher once told me, “The unit circle is just geometry pretending to be poetry.” I didn’t get it then. I kinda do now.
Unit Circle in Trigonometry: Where Angles Learn Manners
When people say Unit Circle in Trigonometry, what they really mean is this is where angles learn how to behave. Each angle measurement, whether it’s in degrees or radians (radians feel weird at first, like wearing someone else’s shoes), corresponds to a point on the circle. That point has coordinates (x, y), and those coordinates are not random. The x-value is Cosine, the y-value is Sine. Just like that. Simple, but also not simple at all when you’re first meeting it.
This is why the circle in trigonometry is sometimes called the trigonometric circle. It’s not just a shape, it’s a translator. It translates rotation into numbers. It turns spinning into something you can calculate, predict, argue about at 2 a.m. before an exam.
And the beauty, if we can call it that without sounding dramatic, is that this works for every angle. Not just the nice ones like 30° or 45°. Even the awkward angles get a seat at the table.
Tangent Trigonometric Function, the One That Refuses to Sit Still
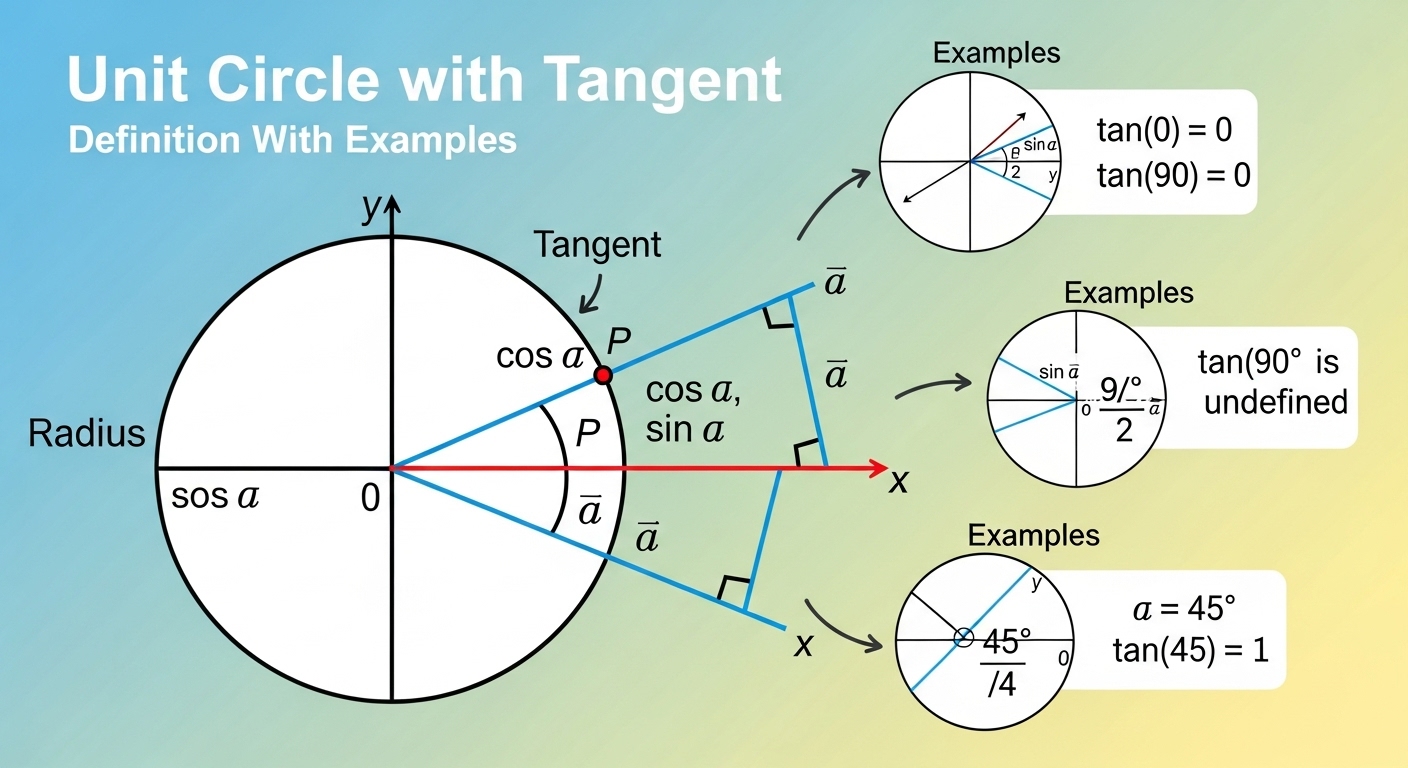
Now let’s talk about Tangent in Trigonometry, which is often misunderstood, like the kid in class who’s actually smart but never does homework the same way. The Tangent function, written as Tan θ, is defined as the ratio of sine to cosine. That’s sinθ divided by cosθ, if we’re being formal, which we are, but only a little.
On the Unit Circle, tangent isn’t represented directly as a coordinate like sine and cosine are. Instead, it’s more like a relationship, a conversation between the x and y values. When cosine gets close to zero, tangent gets dramatic. It shoots off toward infinity, positive or negative, and teachers draw dashed lines and say things like “undefined,” which always feels a bit rude.
But there’s another way to see tangent, one that feels more physical. Imagine drawing a line tangent to the circle at (1,0). The slope of the line that connects the origin to a point on the circle, extended until it hits that tangent line, that length corresponds to Tan θ. This is where slope interpretation sneaks in, tying algebra and geometry together in a slightly awkward handshake.
Unit Circle and Tangent: A Relationship That’s Complicated but Honest
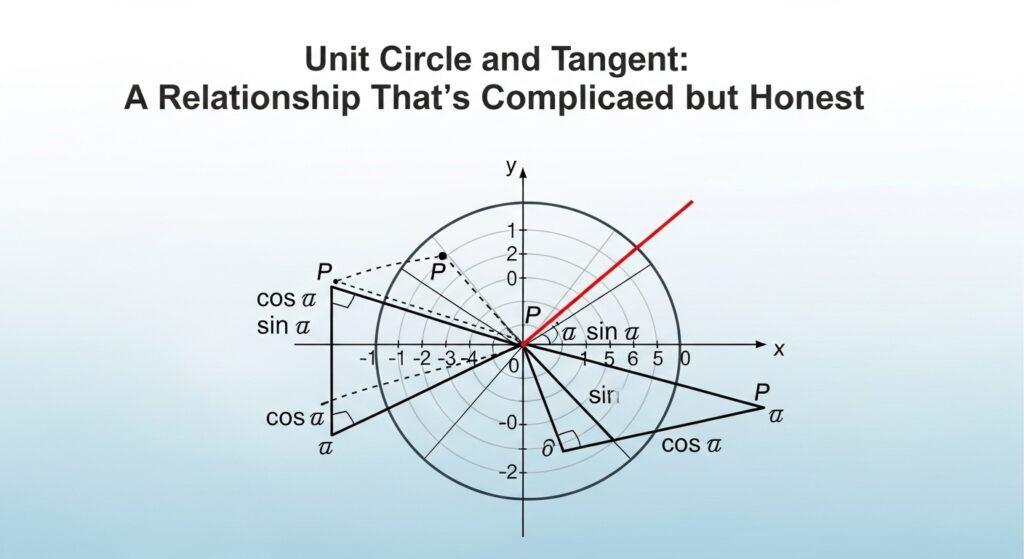
The phrase Unit Circle and Tangent sounds like a chapter title in a book about difficult friendships, and honestly, that’s not far off. The Unit Circle defines the environment, the rules, the space. Tangent reacts to it, sometimes calmly, sometimes wildly. They are connected through angle relationships, and understanding one without the other feels like trying to clap with one hand.
This relationship is crucial for trigonometric problem solving. When you’re asked to find tanθ for a given angle, you’re really being asked to understand where that angle lands on the circle, what sine and cosine are doing there, and how their ratio behaves. It’s less about memorization and more about awareness. A kind of mathematical mindfulness, if that doesn’t sound too strange.
I once heard a parent say while helping their kid with homework, “Oh, tangent is just how steep the angle feels.” Not precise, but weirdly helpful.
Examples That Don’t Feel Like Homework, Almost
Let’s slide into some Examples, gently, without the usual pressure. Suppose θ = 45°. On the unit circle, the coordinates are (√2/2, √2/2). That means Sine and Cosine are equal. So Tan θ becomes 1. Not because the universe says so, but because the ratio says so. Equal over equal is one, even on bad days.
Now take θ = 30°. Cosine is √3/2, sine is 1/2. Tangent becomes 1/√3. That’s it. No drama. The trigonometric ratios behave, everyone goes home.
But then, take θ = 90°. Cosine is zero. Tangent? Undefined. This isn’t a mistake. It’s a boundary. The math is telling you, hey, this slope is vertical, I can’t give you a number without lying. There’s honesty in that.
These mathematical concepts aren’t trying to trick you. They’re trying to be exact, which sometimes feels unfriendly, but it’s actually a kind of respect.
Understanding Angles Through Stories and Small Cultural Notes
In some classrooms in Japan, students physically rotate their bodies to represent angles. In parts of India, teachers draw the Unit Circle in sand, letting wind erase mistakes. A grandmother I met once, who never went to university, told me she imagined angles like turns in a long village road. “Some turns are gentle,” she said, “some make you stop and look.”
Angles are central. The Angle is the heartbeat of all this. Without it, Trigonometric Functions have nothing to respond to. Whether you’re measuring in degrees or radians, whether you love math or tolerate it, angles show up. They always have.
Problems, Practice, and the Quiet Confidence That Comes After

When students talk about Problems in trigonometry, they usually mean the feeling, not the exercise. But solving trigonometric problems using the unit circle builds a strange confidence. You start recognizing patterns. You stop panicking when you see π/3. You remember that sine and cosine are just coordinates, doing their job.
A math professor once said, “If you know the unit circle, you’re never really lost.” It sounded dramatic then. Now it sounds accurate.
Practical Ways to Make Sense of It All
If you’re trying to really learn this, not just pass a test, draw the circle yourself. Badly. Multiple times. Label angles in your own handwriting. Say Sine cosine and tangent out loud like they’re names at a dinner table. Explain the Definition to someone else, even if they don’t care. Especially if they don’t care.
Try connecting mathematical functions to motion. A spinning fan. A clock hand. A door opening. These are not silly tricks. They’re bridges.
Read this Blog: https://wittyeche.com/length-and-width/
Frequently Asked Questions
Unit Circle with Tangent
The unit circle helps visualize the tangent function by showing how tangent values change with different angles on a circle of radius one.
Unit Circle Tangent
In the unit circle, the tangent of an angle is determined by the ratio of sine to cosine at that angle.
Unit Circle Tan
The term “tan” in the unit circle represents the tangent trigonometric function, which describes the slope of a line formed by an angle.
Tangent Unit Circle
The tangent unit circle concept explains how tangent values are measured using angles positioned on the unit circle.
Tan Unit Circle
In the tan unit circle approach, tangent values are found by dividing the y-coordinate by the x-coordinate of a point on the unit circle.
A Gentle Ending, Still Round, Still Ongoing
The Unit Circle doesn’t end. It loops. Every angle eventually comes back around, wiser, maybe a bit tired. The Tangent trigonometric function will keep misbehaving near 90°, and that’s okay. It’s part of its charm, or at least its personality.
If there’s one thing to take with you, it’s this: math is not a wall, it’s a landscape. Some parts are steep. Some are flat. The circle just happens to be one of the places where everything meets. If you’ve got a favorite way of remembering tangent, or a story about finally “getting” the unit circle, share it somewhere, with someone. These concepts grow better when spoken aloud, slightly imperfect, like we all do.