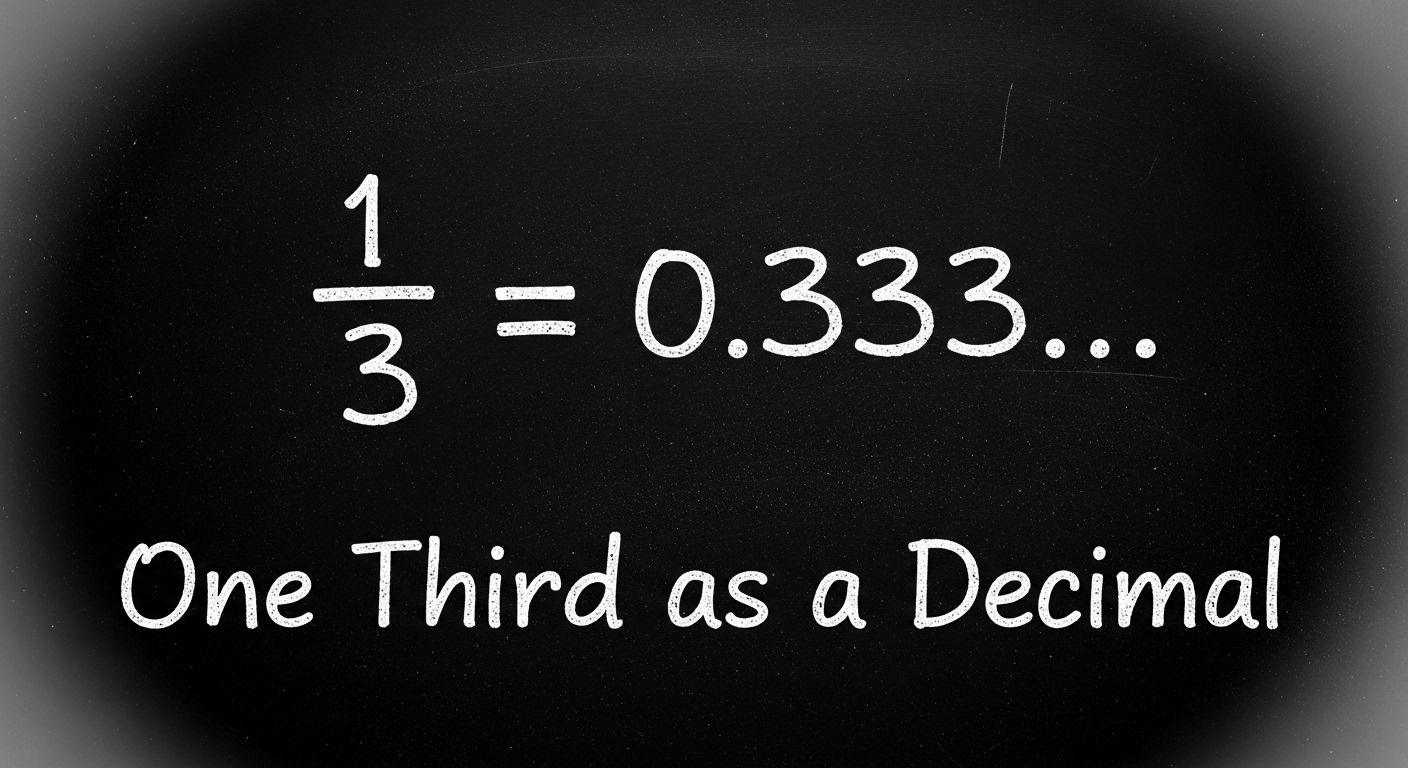I still remember the first time 1/3 made me slightly mad, like a polite kind of mad where you smile but your brain is frowning. I was sitting at a kitchen table, crumbs everywhere, a pencil that didn’t erase properly, and someone said, “Just turn it into a decimal.”
Easy, right? Except it wasn’t. The number kept going. And going. And then, somehow, it was still going. This tiny fraction, barely taking up space on the page, was suddenly infinite, which feels unfair if you ask me.
This article is about that strange magic trick. About what is 1/3 as a decimal, why it behaves the way it does, and why generations of students, parents, and even confident adults have stared at 0.333… and thought, wait, is that… finished? Or is it not.
We’ll wander through fraction to decimal conversion, poke at repeating (recurring) decimals, and maybe, quietly, make peace with the fact that not everything in math wants to end neatly.
If you’ve ever needed math help fractions style, or you’re just curious why some numbers refuse to shut the door behind them, you’re in the right slightly-messy place.
| Aspect | Details |
|---|---|
| Fraction | 1/3 |
| Numerator | 1 |
| Denominator | 3 |
| Division Performed | 1 ÷ 3 |
| Division Method Used | Long division |
| Step 1 | 3 does not go into 1, so a decimal point is added |
| Step 2 | 10 ÷ 3 = 3, remainder 1 |
| Step 3 | Remainder repeats (1 → 10 → 1) |
| Decimal Expansion | 0.333… |
| Type of Decimal | Repeating (recurring) decimal |
| Infinite or Finite | Infinite decimal expansion |
| Reason It Repeats | Remainder repetition during division |
| Mathematical Notation | 0.3̅ |
| Decimal Equivalence | 0.333… = 1/3 |
| Terminating or Repeating | Repeating decimal |
| Base Number System | Base-10 |
| Related Fraction | 2/3 = 0.666… |
| Common Question | Is 0.333… equal to 1/3? → Yes |
What Is 1/3 as a Decimal, Really Though?
So let’s say it plainly, before we get poetic again. 1/3 as a decimal is 0.333…, where the dots mean the 3 never stops repeating. Ever. Not later, not secretly at the end of the universe. It’s an infinite decimal expansion, and it lives comfortably inside the base-10 number system, causing just enough chaos to be interesting.
In proper mathematical notation (repeating bar), you might see it written as 0.3̅, which is math’s way of saying, “Yes, this goes on forever, don’t panic.” This is a classic case of decimal equivalence, where a fraction and a decimal are the same value, just wearing different outfits.
A Math Tutor I once spoke to at Brighterly laughed and said, “Students don’t hate 1/3 because it’s hard. They hate it because it doesn’t finish.” That line stuck with me. Because it’s true, and also kind of poetic, in a nerdy way.
Using the Division Method (Also Known as Long Division Drama)
Let’s walk through the division method, slowly, like we’re carrying a cup of coffee we don’t trust. You take the numerator (1) and divide it by the denominator (3). That’s the core of fraction conversion, nothing fancy yet.
Here’s what happens in long division:
- The dividend is 1
- The divisor is 3
- You add a decimal point and a zero, because 3 doesn’t go into 1 evenly
- 3 goes into 10 three times, with a remainder of 1
- You bring down another zero
- Repeat forever, or until your pencil wears down
This is where remainder repetition shows up like an uninvited guest who never leaves. Every time, the remainder is 1. That repeating remainder creates the repeating decimal. This is the heart of identifying repeating remainders, and once you see it, you can’t unsee it.
That’s the real reason behind why decimals repeat. Not mystery. Not magic. Just a stubborn remainder doing the same thing again and again.
The Pattern Recognition Method, For the Visually Curious
Some people don’t love division. Fair enough. There’s another way, the pattern recognition method, which feels more like noticing music than doing paperwork.
If you know that:
- 1/3 = 0.333…
- 2/3 = 0.666…
- 1/4 = 0.25
- 3/4 = 0.75
You start seeing patterns. Fractions with denominators that play nicely with 10 tend to terminate, while others repeat. This is where terminating vs repeating decimals becomes less of a rule and more of a vibe.
A teacher named Janice S. Armas once said in a workshop, “Patterns are math whispering instead of shouting.” I like that. Because with repeating decimal example cases like 1/3, the pattern is loud once you notice it, but quiet before that.
Why Does 1/3 Repeat Forever?

This question shows up in almost every FAQ (Frequently Asked Questions) list, and for good reason. Why does 1/3 repeat forever? Because 3 has prime factors that don’t match the base-10 number system, which is built on 2s and 5s. That mismatch creates an infinite repeating decimal.
If the denominator, after fraction simplification, only has 2s and 5s, the decimal ends. If not, welcome to infinity. That’s the quiet rule humming underneath decimal representation of fractions.
Or as Franz Jerby Delos Santos once joked during a math tutoring session, “Some numbers are introverts, some are extroverts, and some just never leave the party.” 1/3 is very much the last type.
Is 0.333… Equal to 1/3? Yes, Completely, No Tricks
This one feels like a trap question, but it’s not. Is 0.333… equal to 1/3? Yes. Absolutely. Mathematically, emotionally, spiritually, all of it.
They are decimal equivalence twins. Different forms, same value. If you multiply 0.333… by 3, you get 1. Clean. No leftovers. That’s the proof hiding in plain sight.
Some learners worry the dots mean “almost.” They don’t. The dots mean “exactly, but infinitely.” That’s a big conceptual leap in basic mathematics, and it’s okay if it takes time to land.
How Do You Write Repeating Decimals Mathematically?
This is where notation steps in with a small cape. Instead of writing endless 3s, we use 0.3̅, which is called recurring decimal notation. The bar tells you which digits repeat.
It’s part of learning how do you identify a repeating decimal and how to communicate it without filling the page. In textbooks, worksheets, and decimal practice, this notation saves everyone a little sanity.
Rachelle Bencio Yu, an educator who designs math exercises, once said, “Notation is kindness. It helps the reader breathe.” I think that’s true, especially here.
Do All Fractions Become Repeating Decimals?
Short answer: no. Longer answer: only some. This is the heart of terminating vs repeating decimals, and it matters more than people expect.
- Fractions like 1/4 and 3/4 terminate
- Fractions like 1/3 and 2/3 repeat
- The deciding factor is the denominator’s prime factors
Understanding this helps with fraction practice and speeds up decimal conversion steps because you start predicting outcomes before calculating them.
It’s not guessing. It’s informed intuition, which feels very satisfying once it clicks.
Learning Fractions and Decimals Without Losing Your Mind

If you’re trying to learn fractions and decimals, or helping someone else do it, slow down. Let the weirdness be weird. Use visual models. Use stories. Use mistakes. Especially mistakes.
Many online math tutor platforms now emphasize understanding over speed, and that’s a good shift. Knowing how to divide fractions matters, but knowing why the result looks the way it does matters more.
At Brighterly, tutors often encourage students to explain answers out loud. When someone can say why 1/3 as a decimal repeats, they’ve crossed a quiet but important bridge.
Practical Ways to Make This Stick
Before we close, here are some grounded, human ways to keep this knowledge from floating away:
- Explain fraction division explained style, using food or money
- Practice spotting repeating decimal example patterns without calculating
- Rewrite decimals using mathematical notation (repeating bar) by hand
- Compare decimal form of fractions side by side
- Ask “does this feel like it will end?” before dividing
These aren’t shortcuts. They’re anchors.
Read this Blog: https://wittyeche.com/what-is-80-of-50/
Frequently Asked queestions
what is 1/3 as a decimal
1/3 written as a decimal is 0.333…, where the 3 repeats forever. It is a repeating (recurring) decimal.
how do you write 1 3 as a decimal?
You divide 1 by 3 using long division, which gives 0.333… because the remainder keeps repeating.
1/3 decimal
The decimal form of 1/3 is 0.333… or 0.3̅, showing an infinite repeating pattern.
what’s 1/3 as a decimal
1/3 equals 0.333…, and this decimal never ends, it just keeps repeating the digit 3.
1/3 in decimals
In decimals, 1/3 is written as 0.333…, which is exactly equal to the fraction 1/3, not an approximation.
A Thoughtful Ending, Because Even Numbers Deserve One
So, what is 1/3 as a decimal? It’s 0.333…, yes. But it’s also a lesson in patience, patterns, and the idea that not everything wraps up cleanly. Some truths repeat. Some answers stretch on. And that’s not a flaw, it’s a feature.
If this helped you, or reminded you of a moment when math felt strange-but-interesting, share that experience. Leave a comment. Tell someone else who’s staring at a line of 3s and wondering if they’re missing something. They’re not. They’re right on time.